温暖化対策を分析する／茅 陽一

区>会員, 記>温故知新 (class1957, ローマクラブ, 温暖化対策)

私は、1962年に大学院を修了して、電気機械の講座の講師として電気工学科の教師生活のスタートを切った。というと、普通の人はそれではモーターやインバーター、更にはそれらの応用機械システムの研究教育に明け暮れていたのだろうな、と想像されると思う。しかし、1970年にローマクラブなる組織に接触してから、だいぶ違う世界に飛び込むこととなった。このクラブは、世界を股にかけて活躍する人たちの100人ほどの集まりで、地球の資源環境の有限性を考えると世界の物的な発展をこのままにするとどこかで破綻をきたすという憂いを持ち、それを具体的に解決する方策を探索して世界に提言していこう、という意図で作ったものである。ご承知のように1960年代の終わりに大きな学生運動の盛り上がりがあり、東大も半年ほど殆ど授業の出来ない状態になって、学生の立てこもった安田講堂を警官隊が襲って突き崩す、という形で終わったのだが、私は若い教師であったこともあって、教官側の学生委員となって共闘派の学生との交渉にあたった。そういうことからどうも社会派の教師、と思われたらしく、ローマクラブに参画してその活動を手伝わないか、という誘いがかかってきたのである。

これは地球全体の今後という大変大きな話だったし、自分の関わっていたシステム分析手法をある程度応用していろいろな検討が出来るのではないか、という気がして結局これに参加して研究会を作ってみたり、世界のいろいろなところのローマクラブのシンポジウムに出たりすることになった。

そんな中で、私が関心を持ったのは二酸化炭素（CO2）による温暖化の問題である。これはローマクラブでも真にグローバルな問題の一例として取り上げたのだが、私はこのCO2の濃度が毎年単調に増加している、というハワイでの計測の記録をみせられて、これは何とかしなければならない、と思うようになった。1970から1980年にかけての時期は、気温上昇が世界的にはっきり見えだしており、米国の科学アカデミーや環境省が大々的な調査報告を出すなどして関心が大いに高まった。私も問題が他人事ではない、と思い、一次エネルギーの大部分を化石燃料が占めることを考えると、エネルギー問題の検討が温暖化問題の解決にきわめて重要で、その意味で自分にもいろいろやれることがあるのではないか、と思うようになった。当時の環境庁でも長官をヘッドにした懇談会が出来、いろいろな議論をしたが、結局世界的に議論を進めるべきだとの意見が多数を占めて、国連にグローバルな環境問題を考える委員会を提案すべきだということになり、私もその提案委員の端くれをつとめたりした。この委員会が当時のノルウエイのブルントランド首相が委員長となった環境と開発世界委員会で、Our Common Futureという報告書を出して大変有名になった。この委員会報告でも、CO2問題は大きく取り上げており、そのために1988年にはカナダでサミットの直後、それと同じ会場で「Changing Atmosphere」という会議が開かれ、カナダ首相や先に述べたブルントランド首相が出席して、2005年までに世界のCO2を20％削減しよう、という提案を出して世界で大きな反響があった。私もこれに出席したが、500人の出席者中日本からの出席者が私を含め僅か2人で、日本の無関心さに大変歯がゆい思いをしたことをよく覚えている。

しかし、このような状況からもわかるように、私は温暖化対策には大きな関心があり、当時比較的仲の良かった東大教養学部の村上泰亮教授などからは茅さんはCO2と心中するつもりか、と半分揶揄まじりに言われたほどである。こうした状況のために、1988年末に発足した温暖化に関する政府間パネル（IPCC）には日本政府からいわれて参画することとなった。IPCCは、気候科学に関するWG1、温暖化影響に関するWG2、温暖化対策に関するWG3の３つのグループにわかれたが、私はそのWG3の日本の一員として参加した。

しかし、ワークグループといっても、最初は各国の参加メンバーに温暖化問題の解決が如何に難しい問題か、を理解してもらうことがまず大きな課題だった。そこで、議長に頼まれて私は温暖化対策のむずかしさを、次の簡単なCO2の分解式で説明したのである。

ここでE は一次エネルギーである。この右辺の第一項はエネルギーの炭素依存度、第二項はGDPのエネルギー集約率、第三項は経済レベルを表す。

(1)のそれぞれの項の平均変化率を、Δをつけてあらわすと、(1)から簡単に(2)が出てくる。

こうすると、(2)式右辺第一項はエネルギーの炭素依存度の変化率、第二項は省エネルギー率（マイナスの場合）、第三項は経済成長率をあらわすので、CO2の排出が3つの異なった要因の変化率の和として考えられ、わかり易い。こうしたやりかたは、現在はどこでもいろいろな問題で使う当たり前の式の分解だが、当時はこうするとCO2問題のむずかしさ（つまり、経済成長率というプラスの要因を炭素依存率の低減と省エネルギーで如何に打ち消すか）をよく表す、と理解されて、大変に評判がよかった。この式は、現在でもKaya identityの名で広く知られている。実際、IPCCの最新の第5次報告書でも、WG3においてはこのKaya identityを分析のコアツールにする、という指針が報告書作成のスタートで出されて、大いにこれが使われたと聞いている。

上記は私の関わった一つの例だが、そんなこともあって私は政府の温暖化対策の議論に最初からいろいろ関わることになった。そんな中で、当時の通産省は温暖化を解決するには長期的抜本的な技術開発が重要である、と考え、それを地球再生計画という名で発表した。私も、当時の担当局長と米国にその宣伝の行脚にでかけた記憶がある。

そして、この計画を具体的に進めるために、政府は経団連と相談して（財）地球環境産業技術研究機構、俗称RITEという研究所を発進させ、京都市の協力で京都南端の京阪奈学研都市にその研究所を建設した。この研究所は最初東大工学部長であった近藤次郎先生が所長を引き受けられたが、1998年に、私が慶応大学教授の傍らこの所長を引き受けることとなった。そして、私はその後財団全体の理事長となって現在に至っている。この研究所では温暖化問題の総合的なシステム分析、CO2の回収貯留、バイオテクノロジーによるバイオマス利用などいろいろな研究を推進しているが、私も理事長の傍らそのシステム分析などには折にふれ参加し、意見をいうと共に自分もその研究の中身を勉強するという利点を味わっている。

そんなわけで私はCO2問題の研究に特にここ30年いろいろな形で携わってきたのだが、そんな研究の最近の一つの例をあげよう。それは気候感度の研究である。

本来、気候科学というのはまだまだ未完成な分野で、不確定な要因が多い。将来の温度上昇一つをとっても、こういう対応をとったら何度上昇する、と明確にいえるのではなく、一定の幅の範囲を示すのが通例になっている。したがって、確率論的なアプローチで分析を進める例が多いのだが、最近一つの大きな話題となっているのが「気候感度」の問題である。

「気候感度」とは、大気中のCO2濃度が2倍になったときの大気温度上昇の値をさす。温度上昇は、CO2のような温室効果ガスの大気中濃度の対数に比例的である、とみられているので、上記のような定義が出てきたわけだが、この気候感度については将来の温度上昇の鍵になるパラメータなので、IPCCでもそのスタートの時点からその値が問題となってきた。しかし、その値については次のようにされている。

ここで最良推定値というのは明確な定義がないが、幅のある推定値の中央値とみてよいだろう。ところで、上記にみるように、最新の第5次報告ではその値が定められない、という結果になっている。その原因は、関係する研究者間で意見がどうしても一致しなかった、ということのようだが、もう少し詳しくいうと次のようである。

この気候感度の推定には、いくつかの方法があるが、従来からもっとも使われてきた方法は、世界気候モデル(AOGCM)を動かし、その中でCO2濃度を2倍にして大気温度が一定に落ち着くまでシミュレーションを続け、気温が落ち着いたところでその値を推定値とする、という方法である。しかし、2000年以後、そして特に最近はエネルギーバランスモデル法という全く方法を異にした推定法が広がり、その論文の推定結果が従来からの気候モデル法にくらべ一般に推定された温度上昇が低く出る、という結果になっている。気候モデル法を用いた論文の結果の平均の最良推定値は3.2℃だが、エネルギーバランスモデル法の場合は低いものがかなりあり、たとえばジョージア工科大学のJ.Curryらの論文では、最良推定緒は1.6 ~1.7℃とかなり低い。もし気候モデル法の結果よりCurryらの結果を信ずると、同じCO2の排出に対して温度上昇は半分位、ということになるので、温暖化戦略はおおいに変わってくる。したがって、第5次報告で最良推定値に関して研究者の意見がまとまらなかったのもよくわかるような気がする。

私は、この問題についていろいろ考えたが、いっそ自分でこの気候感度の値の推定をしてみよう、と思い立った。というのも、気候感度に影響する変数はいろいろあるのだが、とにかく地球大気温度と大気中のCO2濃度という基本変数のデータは19世紀中から現在までそろっているのであり、一定の手数をふめば大よその値の範囲はつかめるのではないか、と思うからである。

そこで、次のようにした。

温度上昇をΔT、CO2濃度をCx（ただしXは測定年を示す）、放射強制力の基準年よりの変化をΔFとする。この放射強制力の説明は長くなるので割愛する。すると、従来から次の関係式が成立することが知られている。

(3) (4) をみると、ΔTとln Cx は線形の関係にあることがわかる。

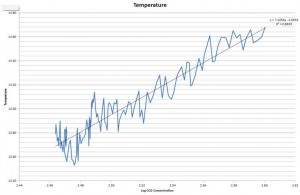
そこで、1880年から2014年までの各年の温度データ、Cx データからΔTとlnCxの線形関係式を最小二乗法で求めた。その結果を、小さい図で恐縮だが次の図に示す。その中での黒い直線が最小二乗法で得られたΔT－ln Cx の一次式である。

>> クリックして拡大図へ

なお、このΔTは、他の温室効果ガスの温室効果とエアロゾルの冷却効果を含んでいるので、その効果分を削減する必要がある。その詳細は略するが、IPCCがそれらのガスのΔFの数値を第5次報告に掲載しているので、それを利用して削減作業を行った。結果は、図のデータ期間である1880年―2014年の黒直線上でのCO2による温度上昇は0.727℃であった。そこで、この値をベースに、黒直線上でln 2 にあたるΔTに拡張すると、

気候感度というのは、実は下のように２つ定義されている。

(5)で求めた値は、詳細は記さないが、TCRよりはやや大きく、ECSより小さい、と解釈できる。一方、ECSとTCRの関係だが、IPCCがその最新の第5次報告の中にIPCCで扱った多くの気候感度に関する論文でのECSとTCRを分析し、その２つの間の関係を統計的に求めている。それによると、上記(5)式の値のTCRに対してはECSは2.6℃程度とするのが平均的と考えられる。また、詳細は略するが上記TCRの定義からしてさきほどの図で求めたΔT2×CO2 はTCRよりはやや大きいと推論されること、を考え合わせると、下記の(6)式が妥当な推定と思われる。

この私の分析は、温度変動に関与する諸種の活動（たとえば火山噴火等）をいわば不規則雑音と解釈してこれに通常の統計分析手法を適用したものであり、気候学者のアプローチとは異なる、いわば工学的分析である。その意味でその妥当性には限界があるかもしれないが、実際の温度とCO2濃度のデータと既知の関係式を利用して行ったものであり、一定の妥当性があると信じている。

以上、やや長くなったが、私の温暖化分析に40年関わってきた状況の一端を紹介させていただいた。電気系学科の卒業生、そして教師の中にもこうしただいぶ毛色の異なった人間がいることを認識していただければ幸いである。

（東京大学名誉教授、クラス1957）

2015年8月18日 区>会員, 記>温故知新